[RBTree lab] ③ Erase

삭제

노드의 삭제는 다음과 같은 과정을 거쳐서 일어난다.

1. 삭제 대상 노드(target)를 트리에서 제거한다.

2. RBTree의 조건에 맞게 트리를 조정한다.

 

1. 삭제 대상 노드(target)를 트리에서 제거

삭제 자체는 BST의 삭제와 동일하게 진행된다.

 

주어진 target이 항상 트리 내에 존재하는, sentinel이 아닌 노드라고 할 때,

target 노드가 제거된다는 것은

target의 연결 관계가 제거되고, 트리에서 target이 차지하고 있던 위치에 다른 노드가 위치하게 되는 것을 의미한다.

 

RB Tree에서는 3가지 경우를 나누어서 노드의 삭제를 진행한다.

1. target의 오른쪽 자식이 nil인 경우

2. target의 왼쪽 자식이 nil인 경우

3. target의 두 자식이 모두 nil이 아닌 경우

 

1, 2번의 경우에는 각각 왼쪽, 오른쪽 자식(nil인 자식의 반대쪽 자식)이 target의 위치를 대체하게 한다.

3번의 경우는 조금 복잡한데, 

target의 오른쪽 자식을 루트 노드로 하는 서브트리에서 가장 작은 값을 가지는 노드가 target의 위치를 대체하게 하거나,

 

target의 왼쪽 자식을 루트 노드로 하는 서브트리에서 가장 큰 값을 가지는 노드가 target의 위치를 대체하게 한다.

그 이유는, 위 그림과 같이 BST의 정의에 인한 것인데, 

이진 탐색 트리에서 어떤 노드 a의 좌, 우 자식 서브트리의 노드들은 모두 a보다 작은값을 가지거나, a보다 큰 값을 가지기 때문이다.

RBTree 또한 BST의 일종이므로 같은 조건을 만족하고,

여기서 구현한 규칙은 왼쪽 자식은 현재 노드보다 작은 값을, 오른쪽 자식은 현재 노드보다 큰 값을 가지도록 구현하였다.

 

따라서 "target의 오른쪽 서브 트리에서 가장 작은 값을 가지는 노드"는 바꿔 말하면

"target의 자손 노드 중 target보다 큰 값을 가지는 노드들 중 가장 작은값을 가지는 노드"이고, 

반대의 경우인 "target의 왼쪽 서브 트리에서 가장 큰 값을 가지는 노드"는

"target의 자손 노드 중 target보다 작은 값을 가지는 노드들 중 가장 큰값을 가지는 노드"인 것이다.

즉 target의 자손 노드 중 target과 가장 가까운 값을 가지는 노드를 찾아내어

target의 위치를 대체하기 위한 과정이라고 할 수 있다.

 

 

💻 구현(6) (transPlant)

먼저 "특정 노드의 위치를 새로운 노드가 대체하는" 기능이 공통적으로 필요하다.

따라서 다음과 같은 함수를 작성한다.

void trans_plant(rbtree *t, node_t *old_node, node_t *new_node) {
    if (old_node->parent == t->nil) {
        t->root = new_node;
    } else if (old_node == old_node->parent->left) {
        old_node->parent->left = new_node;
    } else {
        old_node->parent->right = new_node;
    }
    new_node->parent = old_node->parent;
}

 

이 함수의 기능은 간단하다, 

부모 노드와의 관계 설정을 통해 노드 old_node의 위치를 노드 new_node로 대체한다.

자식 노드는 신경쓰지 않고 단지 부모노드와의 관계만을 변경하는 것이며, 

old_node와 new_node의 위치를 바꾸는 것이 아님을 주의해야한다.

 

💻 구현(7) (subtree_min, subtree_max)

인자로 받은 노드(cursor)를 루트노드로 하는 서브트리에서 가장 작은값 또는 가장 큰 값을 찾는 함수를 구현했다.

노드를 제거하는 경우 중 두 자식 노드가 모두 nil이 아닌 경우에

target노드를 대체할 노드를 찾기 위해 사용된다.

node_t *subtree_min(node_t *cursor, node_t *nil) {
    node_t *min = cursor;
    while (cursor != nil) {
        min = cursor;
        cursor = cursor->left;
    }
    return min;
}

node_t *subtree_max(node_t *cursor, node_t *nil) {
    node_t *max = cursor;
    while (cursor != nil) {
        max = cursor;
        cursor = cursor->right;
    }
    return max;
}

 

💻 구현(8) (erase) (노드의 삭제만 구현된 형태)

특정 노드를 삭제하는 erase함수이다.

앞서 이야기 한 3가지 경우를 기준으로 삭제 방법이 다른것을 확인할 수 있다.

int rbtree_erase(rbtree *t, node_t *target) {
    node_t *y = target;
    color_t y_color = y->color;

    node_t *x;
    if (target->left == t->nil) {
        x = target->right;
        trans_plant(t, target, target->right);
    } else if (target->right == t->nil) {
        x = target->left;
        trans_plant(t, target, target->left);
    } else {
        /** case 1 **/
        /** 삭제 될 target의 자리를 right subtree의 min node로 대체 **/

        // y는 right subtree의 min node
        y = subtree_min(target->right, t->nil);
        y_color = y->color;

        // y는 BST에서 가장 작은 노드이므로 항상 왼쪽 자식이 존재하지 않음(nil)
        // 따라서, x는 y의 하나뿐인 유효한 자식 노드이거나 또는 nil이다.
        x = y->right;

        if (y->parent == target) {  // y가 target의 오른쪽 자식인 경우
            x->parent = y;
        } else {  // 그렇지 않을 경우
            // y의 자리는 y의 오른쪽 자식(유효한 노드 또는 nil임)이 대체하게 하고,
            // target의 오른쪽 자식과의 관계를 y가 대체한다.
            trans_plant(t, y, y->right);
            y->right = target->right;
            y->right->parent = y;
        }
        // 드디어 target의 부모와의 관계를 y가 대체한다.
        trans_plant(t, target, y);

        // 또한, 왼쪽 자식과의 관계 또한 대체하며
        y->left = target->left;
        y->left->parent = y;

        // target이 제거됨으로서 생기는 규칙의 위배를 막기 위해
        // y의 color를 삭제된 target의 색으로 변경한다.
        y->color = target->color;
    }

    free(target);

    init_nil(t->nil);

    return 0;
}

 

 

 

rbtree_erase 함수에서 사용되는 주요 변수의 이름과 역할은 다음과 같다.

 

y

삭제 대상(target의 두 자식 노드 중 하나가 nil일 때) 또는

이동 대상(target의 두 자식 노드 모두 nil이 아닐 때)인 노드이다.

 

x

y의 원래 위치로 이동하여 y를 대체할 노드이다.

x는 y의 하나뿐인 유효한 자식이거나, nil이다.

 

y_color

y의 원래 색상을 저장한다.

y_color를 저장하는 이유에 대해서 CLRS에서는 이렇게 설명한다.

Need to save y’s original color (in y-original-color) to test it at the end, because if it’s black, then removing or moving y could cause red-black properties to be violated.

즉, 삭제에서 제거 또는 이동 대상인 노드 y의 색깔이 BLACK인 경우 RBTree 특성 위반의 원인이 될 가능성이 있기 때문이며

이를 이용해서 뒤이어 설명할 erase_fixup 수행 여부를 결정하기 위함이다.

 

 

left subtree의 max node로 대체하는 방식의 구현은 더보기

    node_t *y = target;
    color_t y_color = y->color;

    node_t *x;
    if (target->left == t->nil) {
        x = target->right;
        trans_plant(t, target, target->right);
    } else if (target->right == t->nil) {
        x = target->left;
        trans_plant(t, target, target->left);
    } else {
        /** case 2 **/
        /** 삭제 될 target의 자리를 left subtree의 max node로 대체 **/
        y = subtree_max(target->left, t->nil);
        y_color = y->color;
        x = y->left;
        if (y->parent == target) {
            x->parent = y;
        } else {
            trans_plant(t, y, y->left);
            y->left = target->left;
            y->left->parent = y;
        }
        trans_plant(t, target, y);
        y->right = target->right;
        y->right->parent = y;
        y->color = target->color;
    }

 

2. RBTree의 조건에 맞게 트리를 조정하기

이 과정이 RBTree의 모든 기능 중 가장 까다로운 부분이다.

y의 원래 색에 따라, 삭제 작업이 완료된 뒤 RBTree의 조건에 맞게 노드 위치의 조정이 필요하다.

 

조건을 위배하는 경우: y의 원래 색 == BLACK

1. y의 색이 RED
2. y의 색이 BLACK

사용자에게 제공될 모든 operation은 RBTree의 조건을 항상 만족하는 상태에서 시작한다는 전제 하에,

색이 RED인 노드를 삭제하는 경우는 RBTree의 조건을 무너뜨리지 않는다.

양쪽 자식이 모두 BLACK이었을 것이기 때문에(조건 4번) 

leaf로 가는 BLACK 노드의 수가 변하지 않고(조건 5번), 

또한 삭제로 인해 조건 4번이 깨지는 것도 아니다.

 

그러나 삭제된 노드의 색깔이 BLACK인 경우에는 조건이 무너지는 경우가 발생할 수 있다.

다시 조건을 보자

1. 모든 노드는 RED 또는 BLACK
2. 루트는 BLACK
3. 모든 리프(NIL)는 BLACK
4. 노드가 RED 이면 그 노드의 자식은 모두 BLACK
5. 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 BLACK 노드를 포함해야함

 

만약, y가 BLACK인 노드라면, 각 조건에 대한 위배 여부는 다음과 같다.

1. 문제 없음
2. y가 루트노드, x가 RED인 경우 루트가 RED가 되어 위배됨
3. 문제 없음
4. x와 x의 바뀐 부모노드가 모두 RED인 경우 위배됨
5. y를 포함하고있던 경로에서 BLACK이 1개 부족하게되어 위배됨

 

2, 4, 5번에서 발생하는 문제를 모두 해결하기 위해서는

x를 BLACK으로 바꿔주면 된다.

 

2번은 경우 루트가 BLACK이 되어 위배가 사라지고,

3번은 부모의 다른 자식 노드는 조건에 부합할 것이고, x만 BLACK이 되면 해결된다.

5번 또한 BLACK이 하나 생겨서 괜찮다...?

 

5번은 안괜찮다. 언제 안괜찮냐, x의 색깔이 원래 BLACK인 경우이다.

이 경우는 5번이 위배되는 상황을 해결하지 못한다.

이중 흑색 노드

이런 상황을 일반화 하여 해결하기 위한 개념적인 도구로서, 이중 흑색 노드(doubly black node)가 등장한다.

위에서 2, 4, 5번 조건이 위배되는 상황을 해결하기 위해 'x의 색을 BLACK으로 "바꿔준다"' 고 하였는데, 

이를 'x에게 extra BLACK을 "추가한다"'고 바꿔 표현해보자.

 

이때, extra BLACK이 추가된 노드의 색(상태)은 둘 중 하나이다.

1. doubly BLACK
2. RED & BLACK

 

 

x의 색이 doubly BLACK 또는 RED & BLACK이 되면

y를 포함하던 경로에서 BLACK이 하나 부족한 상황이 생기지 않게되고,

5번 조건이 위배되는 상황은 사라지지만 1번 조건 "모든 노드는 BLACK 또는 RED"를 어기게 된다.

 

이를 해결하기 위해 x의 색이 RED & BLACK 이 되거나 또는 x가 루트 노드가 될 때까지

 

extra BLACK을 트리의 위로 이동시킨다.

 

만약 x의 색이 RED & BLACK이라면, 색을 BLACK으로 바꾸고,
x가 루트 노드라면 extra BLACK을 제거한다.

 

extra BLACK을 트리의 위로 이동시키기 위해 x와 x의 형제노드인 w가 정의된다.

x는 항상 루트가 아닌 doubly BLACK 노드이다.
w는 x의 형제 노드이며, nil이 될 수 없다(x의 부모 노드에서 조건 5번 위배)

 

x가 왼쪽 자식인지, 오른쪽 자식인지에 따라 2가지 경우가 존재하고

w의 색에 따라서 4가지 경우가 존재하여 총 8가지의 경우가 존재하여, 각 경우에 대한 해결 방법이 다르다.

 

x가 왼쪽 자식인 경우의 4가지 케이스만을 예로 들면, 다음과 같다.

 

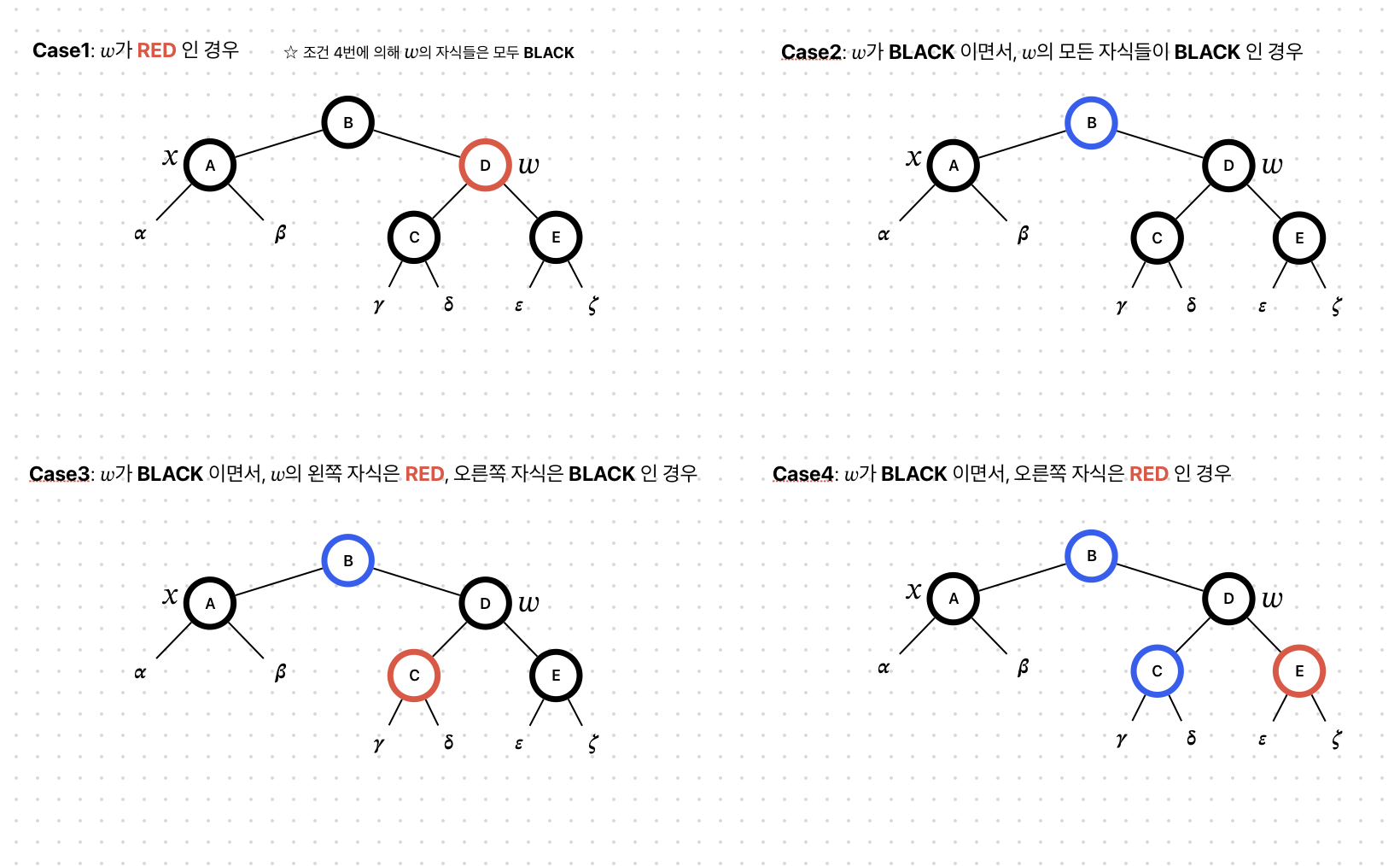
이제 각 경우에 대해 알아보자

 

 

Case 1

먼저, x의 부모노드의 색을 RED로, w의 색을 BLACK으로 바꿔준다.

그 다음, x의 부모를 중심으로 left rotate를 진행한다.

이 상태에서 x의 new w는 rotate전의 w의 자식노드 중 하나이므로, 무조건 BLACK이다.

이제 w가 BLACK인 경우들을 확인해보자.

 

 

Case 2

 

x가 가지고있던 extra BLACK을 

w의 색을 RED로 바꾸고, x가 x의 부모를 가르키도록 한다.

 

 

Case 3

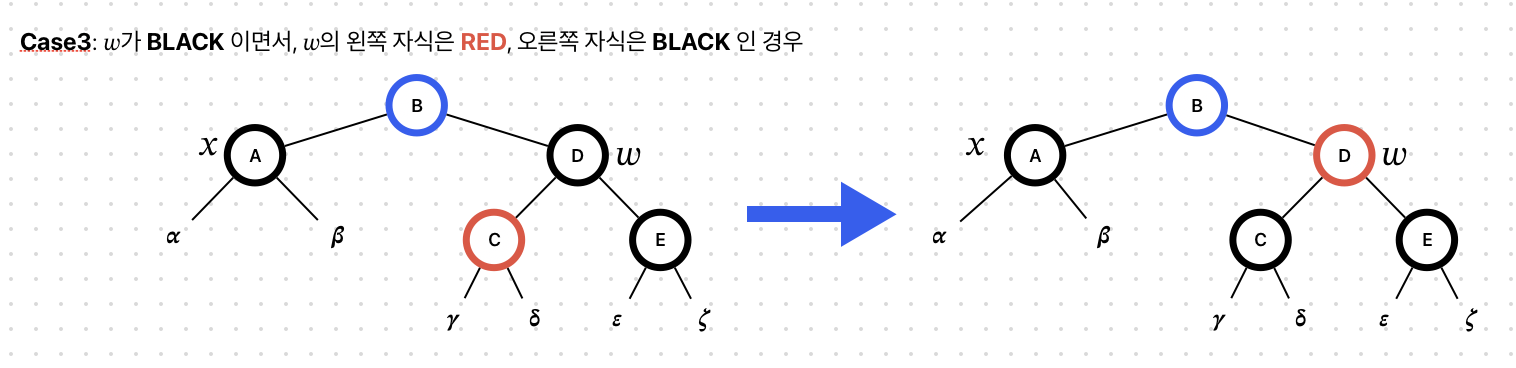
w의 색을 BLACK으로, w의 왼쪽 자식의 색을 RED로 만들어준다.

그 다음, w를 기준으로 right rotate를 진행한다.

이제 w는 BLAKC이며 오른쪽 자식이 RED인 상태가 된다. 

마지막 케이스를 확인하자

 

Case 4

w의 색을 x의 부모 노드의 색으로 만들어주고,

w의 왼쪽 자식의 색을 BLACK으로 만들어준다.

그 뒤, x의 부모 노드를 기준으로 left rotate 한다. 

 

💻 구현(7) (erase-fixup)

void rbtree_erase_fixup(rbtree *t, node_t *cursor) {
    while (cursor != t->root && cursor->color == RBTREE_BLACK) {
        if (cursor == cursor->parent->left) {
            node_t *sibling_node = cursor->parent->right;
            if (sibling_node->color == RBTREE_RED) {
                sibling_node->color = RBTREE_BLACK;
                cursor->parent->color = RBTREE_RED;
                left_rotate(t, cursor->parent);
                sibling_node = cursor->parent->right;
            }
            if (sibling_node->left->color == RBTREE_BLACK && sibling_node->right->color == RBTREE_BLACK) {
                sibling_node->color = RBTREE_RED;
                cursor = cursor->parent;
            } else {
                if (sibling_node->right->color == RBTREE_BLACK) {
                    sibling_node->left->color = RBTREE_BLACK;
                    sibling_node->color = RBTREE_RED;
                    right_rotate(t, sibling_node);
                    sibling_node = cursor->parent->right;
                }
                sibling_node->color = cursor->parent->color;
                cursor->parent->color = RBTREE_BLACK;
                sibling_node->right->color = RBTREE_BLACK;
                left_rotate(t, cursor->parent);
                cursor = t->root;
            }
        } else {
            node_t *sibling_node = cursor->parent->left;
            if (sibling_node->color == RBTREE_RED) {
                sibling_node->color = RBTREE_BLACK;
                cursor->parent->color = RBTREE_RED;
                right_rotate(t, cursor->parent);
                sibling_node = cursor->parent->left;
            }
            if (sibling_node->left->color == RBTREE_BLACK && sibling_node->right->color == RBTREE_BLACK) {
                sibling_node->color = RBTREE_RED;
                cursor = cursor->parent;
            } else {
                if (sibling_node->left->color == RBTREE_BLACK) {
                    sibling_node->right->color = RBTREE_BLACK;
                    sibling_node->color = RBTREE_RED;
                    left_rotate(t, sibling_node);
                    sibling_node = cursor->parent->left;
                }
                sibling_node->color = cursor->parent->color;
                cursor->parent->color = RBTREE_BLACK;
                sibling_node->left->color = RBTREE_BLACK;
                right_rotate(t, cursor->parent);
                cursor = t->root;
            }
        }
    }
    cursor->color = RBTREE_BLACK;
}